超声场及相关物理量分析

 充满超声波的空间或超声振动所波及的部分介质称为超声场。描述超声场的常用物理量主要有声压、声阻抗、声强等。

1. 声压

 假设某一点在没有超声波存在时的静态压强为P0，存在超声波时某一时刻所具有的压强P1，两者之差即为该点的瞬时声压P。声压单位与压强单位相同，均为Pa（帕）。

有效声压是指在一定时间间隔内，瞬时声压对时间取均方根值，即

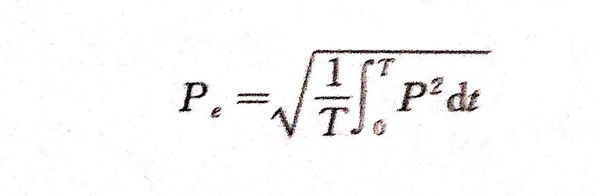
超声波在介质中传播时，介质每一点的声压随时间和振动位移量的不同而变化，所以瞬时声压P是时间和位移的函数，可由下式表达：

 由式（2.1）可知，超声场中某一点的声压按余弦函数周期性变化。声压的幅值与介质的密度、波速、质点振动速度成正比。通常固体介质由于密度大、声速高和质点振速高，导致置于同一超声场中的介质（离声源距离相同），以固体介质中的声压最高，液体中声压次之，气体中声压最小。当然，对于不同固体介质而言，因材料性质、密度、声速等因素的差异，对应的声压也会有所区别。一般认为，探伤仪显示屏上的信号高度与声压成正比。

2. 声阻抗

 超声场中任一点的声压与该处质点振动速度之比称为声阻抗，也称特性阻抗，常用符号Z表示，单位为kg/（m2·s）[千克/（平方米·秒）]：

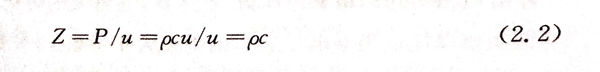
 由式（2.2）可知，声阻抗的大小等于介质的密度与波速的乘积。不难看出，在同一声压下，Z增加，质点的振动速度下降。因此声阻抗Z可理解为介质对质点振动的阻碍作用。类似于电学中的欧姆定律 I=U/R，电压定，电阻增加，电流减少。

声阻抗是表征介质声学性质的重要物理量。超声波在异种介质界面上的反射和透射情况与声阻抗关系密切。

3. 声强

单位时间内在垂直于声波传播方向的介质指定面积上所通过的平均声能量，称为平均声功率或平均声能量流。单位面积上的平均声功率称为声强度，简称声强，通常用符号I表示，单位为瓦／平方米（W/㎡),可写作

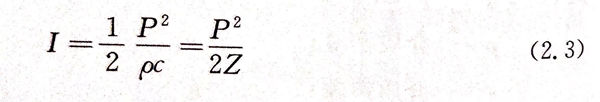
由式（2.3)可知，在同一介质中，声强与声压的平方成正比。

4. 声压级、声强级

 直接使用声压、声强等物理量描述实际生活中的各种声音，数值变化范围会非常宽，涉及的数量级也相差巨大，如果使用对数标度来进行比较计算就能大大简化运算。另一个原因是人耳对声音的接收更接近正比于其对数值，并非正比于强度。因此，在声学中普遍使用对数标度对声压、声强等参数进行度量，对应的，分别称为声压级、声强级，单位用Bel(贝尔）表示，因为贝尔的单位比较大，工程上使用时将其缩至1/10后以dB(分贝）为单位。

 声压级的符号通常用L_p表示。定义声压级为将待测声压的有效值P_e与基准声压P₀。的比值取以10为底的常用对数，再乘以20,即

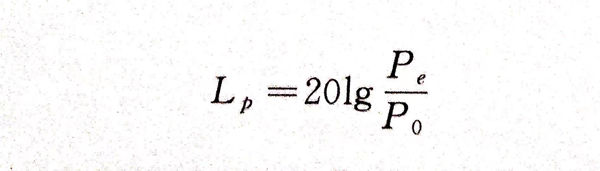
 在空气中，基准声压为P₀=2×10⁵Pa,这个数值是正常人听觉对1kHz声音稍稍感知到的最低声压值，低于此，通常人的听觉系统就感知不到了，亦即听阈声压级为0dB。人耳的听觉从可听阈的2×10⁵Pa的声压到痛阈的20 Pa,两者相差100万倍，而用声压级来表示则变化为0~120dB的范围，使对声音的描述大为方便。

声强级的符号为L_I,定义为待测声强I与基准声强I₀的比值取以10为底的常用对数，再乘以10,即

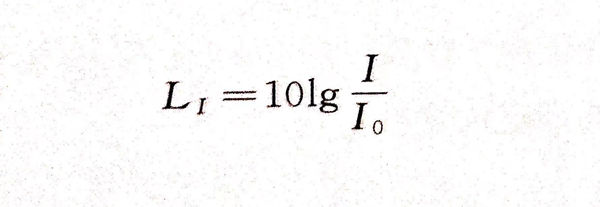
在空气中，基准声强I0取为1×10¹² W/㎡,与空气中基准声压相对应，是能够引起人耳听觉的最低声强。

垂直线性较好的探伤仪，显示屏显示的信号高度与声压成正比，有

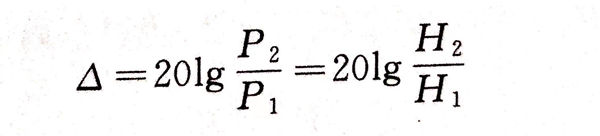
式中，基准声压P₁和基准声强H₁可任意选取。

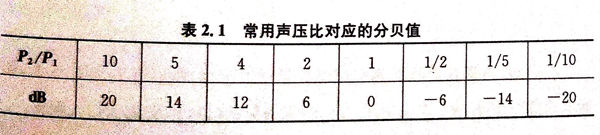
常用声压比（波高比）对应的分贝值见表2.1.