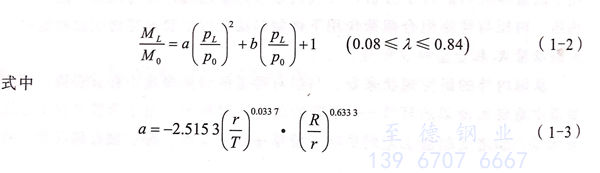1911年,德国科学家Van Karman首先用最小应变能方法研究了不锈钢管弯管加工后的应力应变特性,之后的一些学者都以此方法为基础,仅在级数的取舍等方面作了改进。Clark则认为弯管段为封闭环壳的一部分,通过薄壳方程并以两个变量来表达这些方程,其解与已有解非常接近,且数学处理十分成功,但上述都仅限于弯曲半径较大的情形。Pardue和Vigness,还有 Turner、Ford都研究了弯曲半径较小的情形,给出了整个弯管截面的应力曲线。直到1956年,Kafla和Dunn注意到内压对柔度系数的影响,指出了内压可使弯管的柔度系数降低,刚度增大。Rodabaugh 和 George 利用能量方法研究了内压的影响,给出了影响计算的理论公式。Clark等的计算公式和Rodabaugh等的内压影响修正公式现在被各国规范所广泛使用。
我国在“八五”“九五”科技攻关期间,已基本解决了压力容器、压力管道直管段的塑性极限载荷计算及工程评估问题,但未涉及弯管等复杂结构。鉴于其对管道系统承载能力的重要影响,国家科技部将压力管道元件的安全评估技术列入“十五”国家重大科技攻关的相关项目中。文献给出了薄壁弯管的理论解,文献采用数值分析的方法,对不锈钢弯管结构在复杂载荷作用下的极限与安定分析进行了深入、系统的研究,发展了多组载荷作用下不锈钢管弯管结构塑性极限上限分析的有限元数学规划方法,得出了相应的无搜索优化迭代求解算法,给出了可较好地解决复杂载荷作用下弯管结构与安定分析的数值算法。文献就含局部减薄弯管的极限载荷作了研究,得出了含局部减薄弯管的极限载荷的工程计算方法;文献对在拉、压、弯、扭和内压作用下含缺陷弯管的极限载荷作了研究,得出了弯管在组合载荷作用下的极限载荷的计算公式,能满足一般工程的计算。文献对环向穿透裂纹的斜接弯管进行了有限元分析,计算给出了线弹性条件下,焊制斜接弯管环向穿透裂纹分别在内压、弯矩载荷作用下断裂参量K1的工程应用解;同时以内压、弯矩不同比例的载荷比作用下求解出全塑性J积分值。文献对沿管向穿透裂纹的斜接弯管在内压、弯矩联合作用下的整体应力进行了分析,并利用断裂力学的理论和有限元方法计算了内压、内压与弯矩组合载荷作用下焊制斜接弯管沿管向穿透裂纹的线弹性断裂参量 K1和全塑性J积分。
从国内外的研究现状来看,目前对不锈钢管道的研究多集中在直管段,围绕管道中重要而薄弱的环节-弯管的研究相对较少。由于弯管几何中心线是曲线,加之受制造工艺的影响,管壁往往不等厚,存在截面椭圆化,外拱壁厚局部变薄,内拱壁厚局部变厚甚至出现皱褶等缺陷,当受到内压和弯矩的联合作用时,几何和材料的非线性相互作用,使得弯管的应力状态比直管复杂,因而研究起来也相对复杂。而对超高压弯管还要涉及弯管的应力沿壁厚分布不均匀和应力集中的现象,因而对超高压弯管的研究就更加复杂,目前对超高压弯管的研究文献资料报道得很少,而现有的文献资料报道得最多的是超高压弯管的加工与制造工艺,对超高压弯管的受力分析及工程中的应用的研究报道只有杨家瑞在文献中提到了超高压弯管的极限载荷的计算方法。2010年,毛苗等人对受内压作用下的90度大型厚壁弯管进行了应力计算分析及试验研究,得到了弯管的应力分布规律。2011年,乐增等人应用双剪强度理论推导出求解不锈钢管弯管的极限载荷一般公式,如式(1-1)所示。

2014年,朱倩等人基于统一强度理论,考虑中间主应力效应及拉压不等特性,建立了等壁厚、变壁厚及局部减薄压力弯管的极限内压统一解,研究了统一强度理论参数、拉压比、弯曲系数和不锈钢管弯管壁厚对统一解的影响特性,结果表明:弯曲系数、强度理论参数等因素对极限内压曲线的影响显著,考虑中间主应力效应能充分发挥材料的强度潜能。李建等人考虑几何和材料的非线性相互作用,采用有限元方法研究了复杂载荷下不锈钢弯管的极限载荷,提出了弯矩以及内压、弯矩联合作用下的极限压力、极限弯矩与弯管几何尺寸的定量关系如式(1-2)。