超声波在不同介质界面处的反射、折射和透射

 超声波在不同介质界面处的反射、折射和透射情况是进行超声探伤的重要物理基础。声波能量经界面时的声压声强变化主要取决于两侧介质的声阻抗。

1. 超声波垂直人射到两种介质界面处的反射透射情况

 当超声波垂直入射于两种不同声阻抗介质的界面时，其反射波按入射波相反的路径返回，透射波垂直进入第二种介质。假设超声波所处介质声阻抗为Z₁,人射声强为I₀,入射声压为P₀,反射声强为I_r,反射声压为P_r;另一种介质声阻抗为Z₂,透射声强为I_t,透射声压为P_t.令声阻抗比m=Z₁/Z₂,可得：

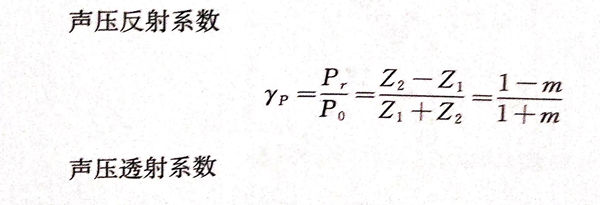
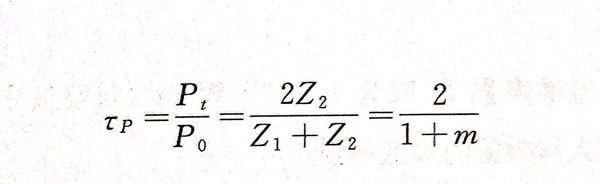
声压视为平面上单位面积所受的力，那么平面两侧的力应当平衡，故声压变化有P₀+P_r=P_t.结合声压反射、透射系数，有

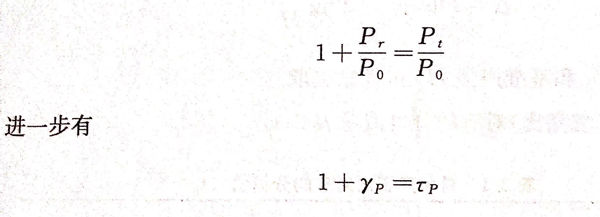
类似地，声强在界面两侧应满足能量守恒定律，所以有I_o=I_r+I_t,如果把声强反射率（R)定义为I_r/I₀,声强透射率（D)定义为I_t/I₀,则有：

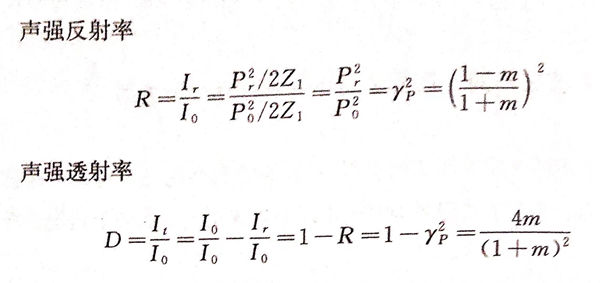
 实际检测中，常用到自发自收探头，例如对钢板进行检测时，认为声波垂直入射进人钢板内部，透射波到达底部后，声压在钢板／空气界面被完全反射，然后垂直返回，被探头接收。探头接收到的返回声压P'_t与人射声压P₀之比称为声压往复透过率，常用符号T_p表示。

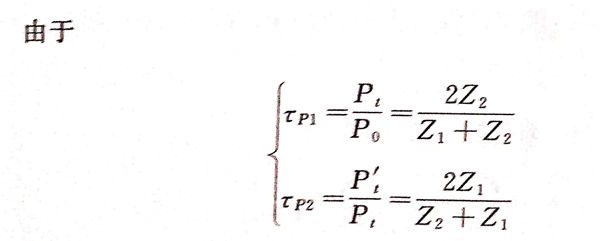
所以

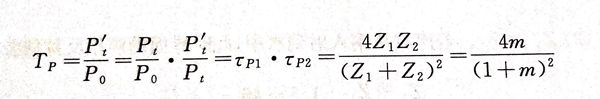
对比声强透射率D和声压往复透过率T_p,可知两者在数值上相等。

超声波垂直入射于不同声阻抗介质的界面，有以下四种反射和透射情况。

a.  Z₁<Z₂

 若声波从水中入射到钢中，水的声阻抗为Z1=1.5×106kg/(㎡·s),钢的声阻抗为Z2=46×106kg/(㎡·s),水／钢界面上的

 图2.9表示从水入射到钢时，声压在两侧的分布。当声波从声阻抗小的介质人射到声阻抗大的介质时，反射声压较入射声压略低，而透射声压高于入射声压，且等于两者之和。由声强透射率D的大小可知入射声强中只有12.24%的能量进入钢中。

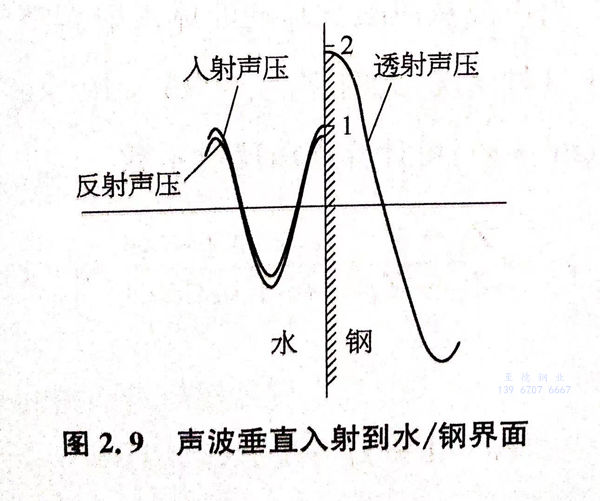
b. Z₁>Z₂

若声波从钢入射到水中，此时界面的声压反射系数

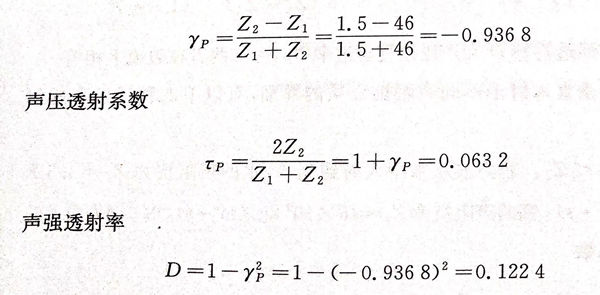
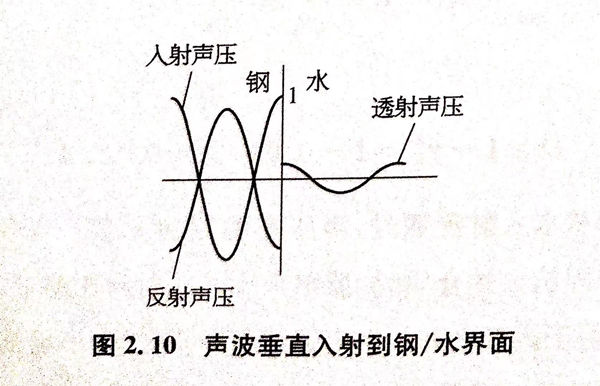
图2.10表示从钢入射到水时，两侧的声压分布。当声波从声阻抗较大的介质入射到较小的介质时，反射声压较入射声压略低；而透射声压因入射声压与反射声压相位相反，其数值也较小。计算得知入射声强中同样有12.24%的能量进入水中。

c. Z₁ ＞ Z₂

 当声波从声阻抗高的固体入射到空气中，例如从钢中入射到空气中，就属于这种情况，此时Z₁(钢）＝46×10⁶kg/(㎡·s),Z₂(空气）＝0.0004×10⁶kg/(㎡·s),可计算声压反射系数

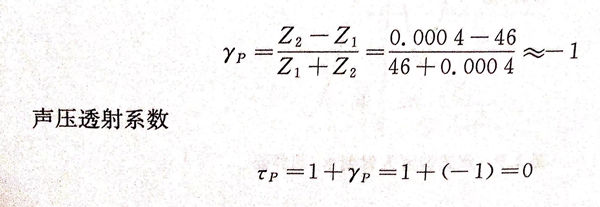
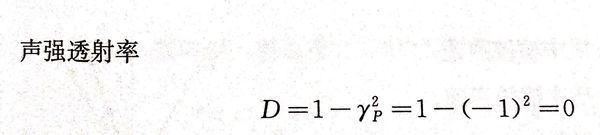
 此时，声波在界面处几乎全部被反射，无法透射到空气中，因此，当超声波探头与粗糙待测件表面接触，如果不加耦合剂，就相当于探头与待测件表面间有一层空气，导致声波能量无法透射到待测件中，无法进行探伤。

d. Z₁≈Z₂

 当声波从两种声阻抗相近的介质界面经过时，例如普通碳钢焊缝金属与母材金属之间，声阻抗相差仅1%,此时，界面的声压反射系数

此时，在界面处反射声压极小，而透射声压几乎与入射声压相同；声波能量几乎全部透射到第二种介质中。

2. 超声波斜入射到两种介质界面处的反射折射情况

当超声波以一定角度斜入射到两种介质界面时，会发生反射和折射现象，且遵循反射和折射定律。一定条件下，还会发生波型转换现象。

 a. 超声纵波斜入射

当超声纵波斜入射到两种介质界面时，反射波和折射波的传播方向符合反射定律、折射定律，如图2.11所示，即

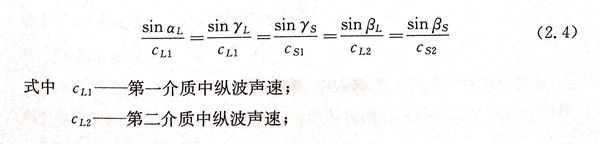
 由式（2.4)可知，在同一介质中声波纵波波速不变，因此纵波反射角与纵波入射角相等，即α_L=γ_L,同时，同一介质中纵波声速大于横波声速，因此纵波反射角大于横波反射角，纵波折射角大于横波折射角，即γ_L>γ_s,β_L>β_s.

当α_L增加时，β_L也增加，增加到一定程度时，β_L=90°,这时所得纵波入射角称为第一临界角，常用a_I表示。当α_L>α_I时，第二介质中既有折射纵波L,又有折射横波S.

当α_L增加时，β_s也增加，增加到一定程度时，β_s=90°,这时所得纵波入射角称为第二临界角，常用a_II表示。当α_I<α_L<a_II时，第二介质中没有折射纵波L,只有折射横波S,这种情况也是横波探头的制作原理。

b. 超声横波斜入射

当横波以一定角度入射到两种固体界面时，也会出现波形的转换，如图2.12所示。

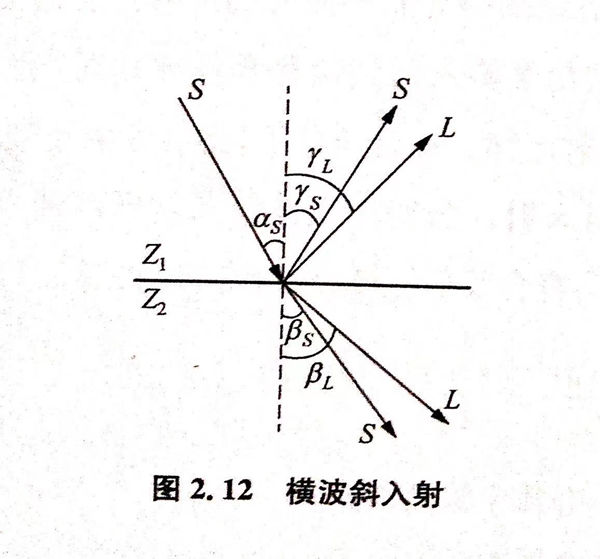
同样地，横波斜入射也符合反射、折射定律：

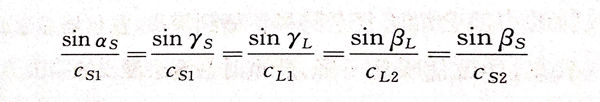
横波斜入射时，随着α_s增加，y_L=90°时，所对应的横波人射角α_s为第三临界角，常用α_III表示，横波入射角大于第三临界角时，产生横波全反射现象。