目前,研究不锈钢应力腐蚀概率的模型有两类,随机变量模型和随机过程模型。
1. 随机变量模型
该模型是在确定论基础上发展起来的。首先确定系统退化特征值,然后再建立特征值与相关变量的关系式,再将公式中的变量看成随机变量,最后通过相应的计算方法得出结果。随机变量是影响特征值的一些重要物理量,可以是自变量,也可以是因变量,还可以是无关变量。随机变量可分为离散型随机变量和连续型随机变量,离散型随机变量具有分布律,连续型随机变量具有概率密度函数f(x)以及概率分布函数F(x),分布律和分布函数可分别描述不同类型随机变量的概率特性,对于研究应力腐蚀随机性中的随机变量一般都是连续型的,如材料性能、环境中离子浓度、温度、载荷等。确定随机变量分布类型以及参数是概率研究的重要内容,它们将直接影响失效概率的计算结果及其精确度。因此,随机变量的概率分布特性研究是一项基础性的研究工作。一般由观测数据确定随机变量概率分布类型,并在此基础上确定其参数;当由已有的观测数据难以确定该随机变量的理论分布形式时,则定义一个实验分布,再进行拟合检验,最后根据有限比较法选择其中的最优概率分布类型作为参数的概率分布类型。正态分布、Weibull分布、指数分布以及Poisson(泊松)分布等都是应力腐蚀概率分析中常用的概率分布类型。
参数估计的方法有矩估计法、最大(极大)似然法、最小二乘法和贝叶斯估计法,其中矩估计法、最大(极大)似然法最为常用。矩估计法对任何总体都可以用,不需要事先知道总体的分布,方法简单,但是,变量分布特征没有得到有效使用,一般情况下,该方法的估计量有多个。最大似然法是在总体类型已知条件下使用的一种参数估计方法,认为未知参数的估计值应使样本观测值出现的概率最大。有些随机参数总体服从什么分布是未知的,我们要对总体是否服从某种分布作检验,这样的检验称为分布的检验。常用的样本概率分布检验方法主要有:χ2检验、J-B检验、A-D检验、K-S检验以及正态分布的概率纸检验等。χ2检验法可适用于离散型或连续型分布,是一种应用比较广泛的分布检验法。
2. 随机过程模型
随机过程按统计特性可分为平稳随机过程和非平稳随机过程,按照记忆特性可分为纯粹随机过程、马尔科夫随机过程和独立增量随机过程;按概率分布函数可分为高斯随机过程和非高斯随机过程。平稳随机过程是一类基本的、重要的随机过程,实际工程领域所遇到的很多概率问题都可以认为是平稳随机过程,平稳随机过程的统计特性不随时间的变化而发生变化,也就是说,对于时间t的任意n个数值t1,t2,···,tn和任意实数r,如果随机过程X(t)的n维分布函数满足如下关系式,则X(t)称为平稳随机过程。
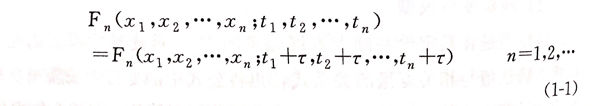
在研究应力腐蚀随机性问题中,泊松过程和马尔科夫过程是常用的两种随机过程:
①. 泊松过程是一种重要的独立增量过程,是服从泊松分布的离散随机过程。其应满足两个条件。不同时间区间内所发生事件的数目是相互独立的随机变量;在时间区间[t,t+Δ]内,发生事件数目的概率分布为:
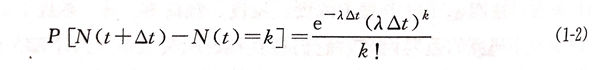
式中,λ为强度因子,表示单位时间内事件发生的平均数。
齐次泊松过程(homogenous Poison process,HPP)属于平稳增量过程,因此,λ为一正常数,且均值E[X(t)]=λt.平稳增量过程有时并不适合描述腐蚀的实际情况,因此引入了非齐次泊松过程(non-homogenous Poisson process,NHPP).在非齐次泊松过程中,强度因子成为一个与事件有关的强度函数λ(t), 代表了不同起始时间段事件发生的数目。事件在Δ时间内发生k次的概率为:
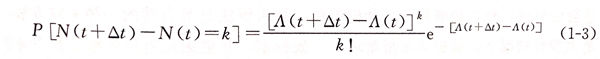
②. 马尔科夫过程是一种应用极为广泛的随机过程,常用来研究材料的退化过程。该过程具有如下特性,在已知目前状态X(t)条件下,它未来的状态X(u)(u>t)不依赖于以往的状态X(v)(v<t),只取决于当前状态,即:
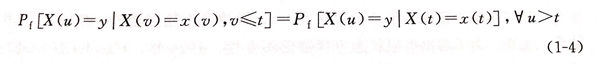
在随机过程研究中,通常把状态和时间离散化,这种马氏过程称为马尔科夫链(Markov chain,又称马氏链)。对于马尔科夫链,最重要的是确定所有状态间可见的两两转移概率,假设一个马氏链总共有N个状态,则其状态转移概率为一个NXN的矩阵,由一步转移概率可以写出其转移矩阵为:
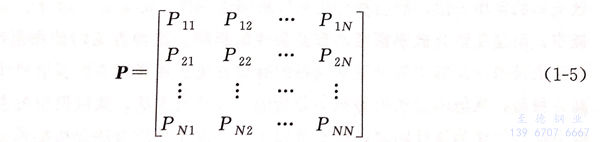
理论上,马尔科夫过程能很好地满足工程实际,但在实际应用中会遇到不少问题,主要有两个难点:实验数据的测量和转移概率的计算。
3. 失效概率计算
根据可靠性理论,把结构的可靠和失效两种工作情况的临界状态称为结构的极限状态。GB 50153-2008 中对结构极限状态的定义为:整个结构或结构的某一部分超过某一特定状态就不能满足设计规定的某一功能要求,此特定状态为该功能的极限状态。当结构丧失了规定的功能时,就认为失效。广义的“失效”认为只要出现以下三种情况就是失效:
①. 完全不能工作(完全丧失功能);
②. 虽仍能工作,但不能完全满足规定的功能(功能衰退);
③. 能工作和完成规定功能,但不能确保安全,应更换维修。
结构的极限状态方程为:
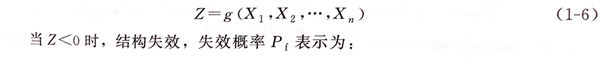
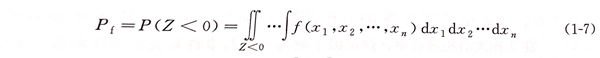
失效概率的求解方法主要有三种:一是解析解法;二是近似解法;三是数值解法,包括数值积分法和模拟法。解析解法是最直接的一种求解方法,但绝大多数情况下,解析解法很难求出失效概率,只能采用近似解法,其中最常用的是一次二阶矩法。对于应力S和强度R都服从正态分布的情况,采用一次二阶矩法计算可靠性系数β,一旦得到可靠性系数,失效概率可由下式计算:
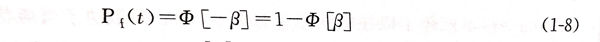
一次二阶矩法存在一定的局限性: 一般情形下精度较差;极限状态方程缺乏不变性。为了解决极限状态方程缺乏不变性,1974年,Hasofer与Lind 对一次二阶矩法进行了改进,后被称为改进的一次二阶矩法,也称为H-L法。
前两种方法都是针对服从正态分布的随机变量,而在实际工程问题中,很多随机变量往往为非正态分布,针对这种情况,Fiessler等提出了量正态分析法,这种方法可适应于求解任意分布随机变量的失效概率。数值解法是求解失效概率的常用方法,数值积分法和解析解法一样,都是直接积分求解结构的失效概率,但是受联合概率密度函数复杂性的影响,这种方法的使用范围受到限制;而数值模拟法是解决复杂概率问题的有效方法。随着计算机容量和计算速度的提高,目前,数值模拟法成为概率分析的一种普遍方法,数值模拟的主要作用是把概率模型转化为统计问题,以便可以采用标准统计学方法分析结果。蒙特卡罗模拟法是一种传统的计算方法,它的基本思想是用基本随机变量的联合概率密度函数进行抽样,用落入失效域内样本点的个数与总样本点的个数之比作为所定义的失效概率。该方法不受随机变量维数限制、不存在状态空间爆炸问题,且不受任何假设约束,可以用来解决高维动态失效概率的求解难题,当抽样试验次数足够多时,近似解的精确度高,是目前应用最多的一种数值模拟方法。



