随机变量模型和随机过程模型是研究应力腐蚀概率的常用模型,本章重点介绍随机变量模型。
一、应力-强度干涉模型
1942年,Pugsley提出了采用应力、强度分布函数曲线的干涉区面积分析失效概率的方法,即应力-强度干涉模型,该模型在构件和系统的可靠性分析中得到了广泛应用。目前,已成为分析构件和系统失效概率的重要模型之一。在结构可靠性分析中,应力-强度(S-R)干涉模型应用最广,模型中的S和R的含义不仅仅是力学分析中的应力和强度,二者具有更广泛的范畴。对于一个系统而言,S指的是造成结构破坏的所有因素,即推动力;R代表了结构抵抗破坏的能力,即阻抗力。
应力腐蚀断裂是一种低应力脆断,是断裂和腐蚀两种机理相互影响的结果。因此,当应力还远低于断裂应力时就能引起应力腐蚀裂纹的产生和扩展。应力作用降低了材料的耐腐蚀性能,而腐蚀降低了材料的断裂强度,两者是互相促进的。也就是说,机械力和化学力的协同作用导致了裂纹的扩展,如果只有应力或腐蚀单独作用,是不会出现应力腐蚀断裂的结果。应力腐蚀断裂要经过一定的时间才能发生,这是因为能量积蓄到使材料破坏的程度是需要时间的,应力腐蚀是使材料强度逐渐退化的过程,因此,我们可以采用耐久性损伤模型来描述应力腐蚀失效的物理过程。由S-R干涉模型的理论可以写出结构的极限状态方程


因此,对于失效概率的研究就转化为对强度和应力由于概率分布干涉引起的状态失效问题的研究。当fs(s)和fR(r)分别表示应力和强度的概率密度函数时,图中两者重叠部分面积反映了失效概率的大小,如图6-1所示。
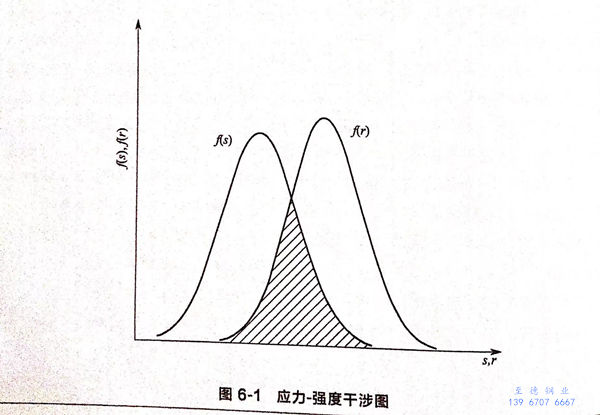
假如最初应力与强度是留有充分的安全余量的,那么经过一定时间后,随着应力分布与强度分布的交叠,就有失效发生,这种情形可以说是耐久模型的典型例子。根据应力-强度干涉模型不但能够求解应力腐蚀失效概率,还可以分析应力腐蚀不同阶段的概率情况,如裂纹的萌生概率、裂纹的扩展概率等。
当材料发生腐蚀后,随着时间的推移,材料抵抗破坏的能力降低,而腐蚀环境很可能变得更加苛刻。例如应力腐蚀,随着裂纹的扩展,材料强度降低、裂纹尖端应力集中区域增大,局部存在侵蚀性离子的富集,使得广义应力变大而强度降低,此时S(t)和R(t)都是与时间有关的变量,很显然,概率密度函数也着时间的变化而变化。当强度随时间发生衰退时,强度和应力组成的干涉区域随时间变化会越来越大,这意味着产品可靠性在降低。
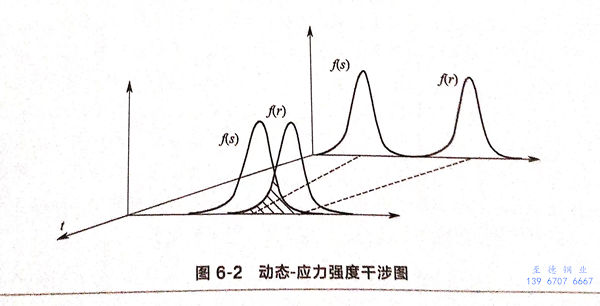
大多数参数的不确定性与时间有关。发生应力腐蚀时,构件所受的广义应力一般是随机过程,应力称为时间的函数,强度为一固定的临界值,如图6-2所示,功能函数应表示为

二、应力腐蚀参数的概率分布估计
1. 变量分布类型确定
采用S-R模型分析应力腐蚀失效概率时,第一步是确定应力腐蚀的“推动力”,即S所包含的参数,包括温度、侵蚀性离子浓度、pH值等,分析各参数的分布概型。在进行参数的概率分布类型研究中,一般经过以下步骤:①. 假设随机变量服从某一分布;②. 在假设分布基础上构建统计量;③. 根据统计量的分布做出统计推断,进行拟合检验;④. 选择最优概型。常用的统计量包括均值、标准差、极差、变异系数、偏度等。正态分布、威布尔(Weibull)分布、指数分布以及Poisson分布等都是应力腐蚀概率分析中经常用到的随机变量的概率分布类型。
通常,直接计算概率的密度函数难度非常大,常用的处理方法是把概率密度估计转化为参数估计问题。因此概率密度函数的确定是关键,正确的密度函数是获得准确估计值的重要前提。
2. 参数的估计和假设检验
由于正态分布情况发生的比较多,因此,以正态分布为例加以说明。参数估计的思路是采用样本统计量估计总体参数。常用的参数估计方法有矩估计法和最大(极大)似然法,除此之外,还有最小二乘、贝叶斯估计等方法。矩估计法不受变量分布的影响,这也恰恰成为该方法的缺点,即变量的分布信息不能被充分利用,一般具有多个分析结果。与矩估计法相反,最大似然法的使用受已知变量概型的影响,必须在已知概型的前提下才能使用,而且假设的概率模型正确性对参数估计结果影响很大。最大似然估计法具有计算简单、收敛型好等特点,在参数估计中的应用更加广泛,其主要计算步骤如下:

式(6-10)称为似然方程组,求解该方程组,得出均值、方差最大似然估计值
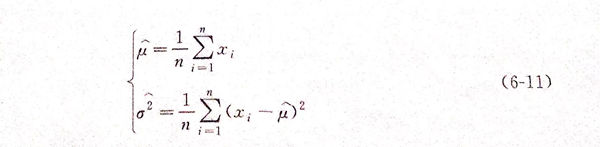
以上过程是参数估计,下面对参数假设检验。与参数估计的目的相同,参数假设检验也是根据样本信息对总体的数量特征进行推断。
假设检验是以样本资料对总体的先验假设是否成立,根据样本的统计量检验假设的总体参数的可靠度,同时做出判断结果,判断结果包括接受和拒绝。分析过程是:①. 提出原假设(要求检验的假设)H0 :F(x)=F0(x)和备选假设(如果原假设不成立,就要接受另一个假设)H1:F(x)≠F0(x);②. 选取恰当的检验统计量;③. 计算观测值;④. 确定显著性水平;⑤. 依据检验统计量观测值的位置给出判断结果。
在以上分析过程中,可能会犯两类错误:当H0为真时而拒绝H0,称为第一类错误;当H0为假时而接受H0,称为第二类错误。犯两类错误的概率通常是矛盾的:一个概率小了另一个概率就大。在实际使用中,我们一般限定犯第一类错误的概率不超过给定的α,使犯第二类错误的概率就可能小。在正态总体参数的假设检验中,主要包括均值的U检验和t检验、方差的χ2检验等。
3. 分布的假设检验
上一小节介绍的是在总体分布已知的情况下,对分布中的一些未知参数进行检验。但是,很多时候并不知道总体的分布规律,我们往往是根据样本来假设总体的分布类型,因此,对于总体样本所假设的分布是否正确,还需要检验,常用的有χ2、J-B、A-D、K-S等检验方法,其中χ2检验应用较多,下面以这种方法为例,介绍检验过程。
χ2检验法的分析过程是:①. 提出原假设;②. 检验假设H0:Fx(x)=F0(x;θ1,θ2,··,θm).先用若干个互不相交的小区间把样本数据进行分组,通常每个区间的数据不少于5个,若不满足这一要求,可以通过合并区间来达到这一要求。假设H0成立,根据分组结果计算χ2检验统计量
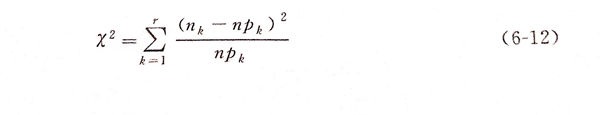

4. 主要参数的概率分布
根据以上分析步骤,对应力腐蚀环境中的离子浓度的统计性进行分析。数据来自某石化企业的监测数据。频率直方图要将样本值分为r个不相交的区间,r值可由 Sturges公式确定,并取整数。r值取决于样本数n。
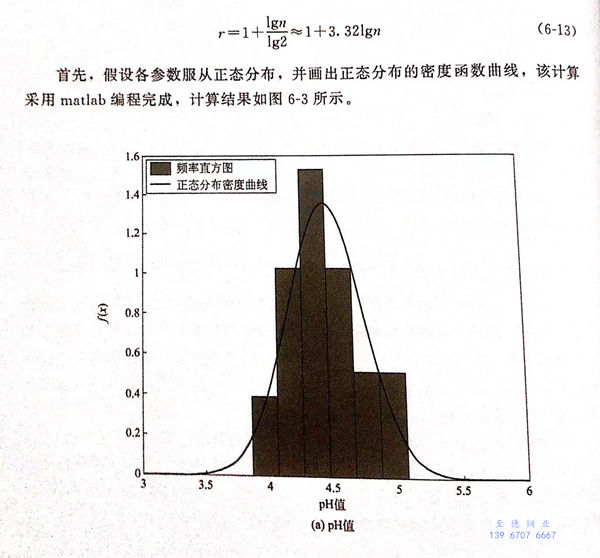
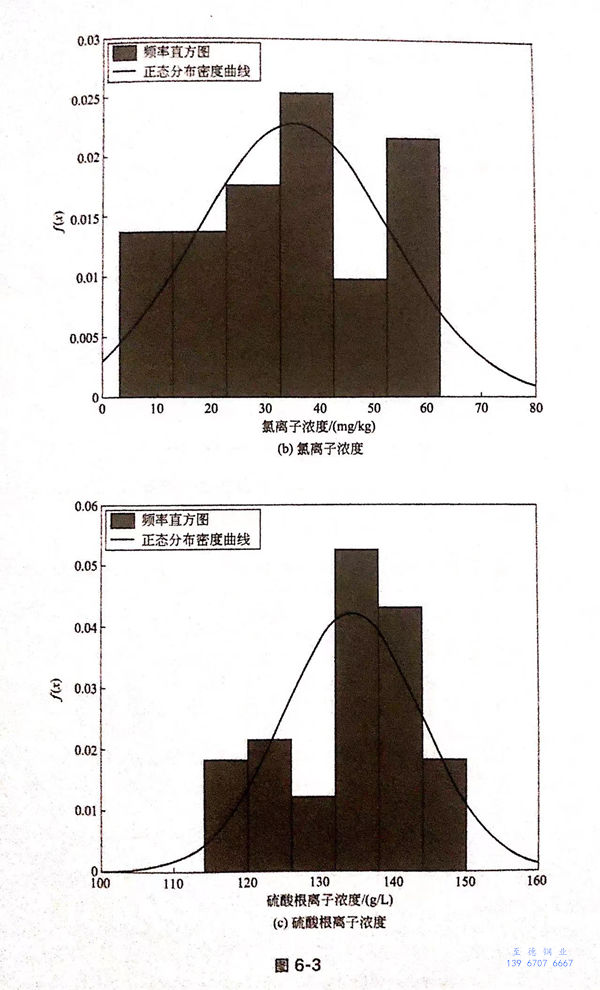
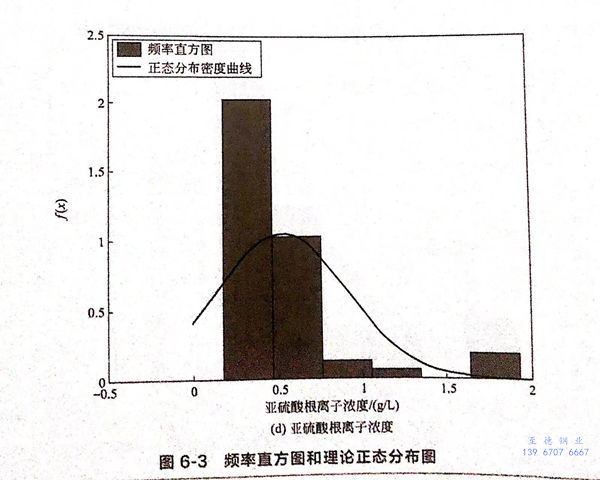
首先,假设各参数服从正态分布,并画出正态分布的密度函数曲线,该计算采用matlab编程完成,计算结果如图6-3所示。
从图6-3可以看出,pH、氯离子浓度和硫酸根离子浓度满足正态分布,而亚硫酸根离子浓度不满足正态分布,经过分析,认为满足威布尔分布,如图6-4所示。
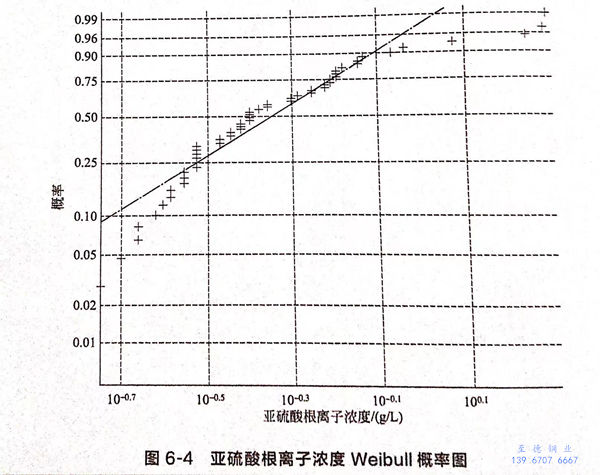
经过卡方检验,在显著性水平0.05下,可以认为:
温度服从N(98.25,1.642);
pH服从N(4.4608,0.29522);
硫酸根离子浓度服从N(143.5204,9.48592);
氯离子浓度服从N(35.3481,17.57352);
亚硫酸根离子浓度服从α=0.5926,β=1.5746的两参数威布尔分布。
亚硫酸根离子浓度服从威布尔分布的原因:亚硫酸根不稳定,与氢离子反应,从而浓度逐渐减小。
三、失效概率计算方法
1. 解析法
当应力和强度是比较简单的变量时,式(6-4)可以直接计算失效概率。在一些研究中,会出现“干涉面积=失效概率”的说法,这种说法是不正确的。根据可靠性理论可知,应力-强度模型中强度大于应力的概率即为可靠度。可靠度P可根据下式计算
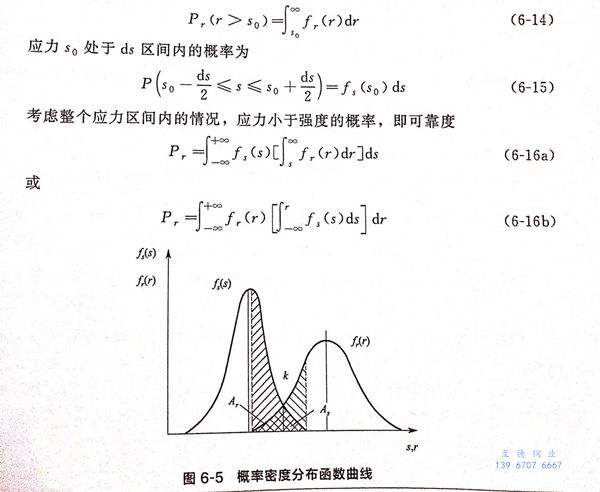
从计算结果可以看出,失效概率远小于干涉面积之和。


2. 数值解析法
当随机变量较多时,直接求解失效概率值是很困难的,采用数值求解是一种比较好的解决方法。在应力腐蚀概率计算中,涉及的随机变量较多且具有不同的分布类型,结果难以用解析法和近似法求解,可以采用蒙特卡洛(Monte-Carlo)模拟法。Monte-Carlo模拟法的特点是:①. 受研究问题维数的影响较小;②. 不受假设约束;③. 不存在状态空间爆炸问题;④. 不受变量数量的影响。因此,Monte-Carlo法是一种处理高维动态失效概率问题的方法。
蒙特卡洛模拟法又称为随机模拟法,基本思想是:




