作为应力腐蚀裂纹的萌生源,点蚀的产生以及生长过程相当于裂纹的孕育期。目前,对于点蚀的萌生机理有很多说法,每一种机理都得到了相当多的实验支持。点蚀萌生机理虽多,但是建立的相应判据却很少。点蚀的萌生和生长受很多因素的影响,如腐蚀介质的成分、温度和流动状态,材料的力学性能、表面硬质夹杂和粗糙度,这些物理量的不确定性使得点蚀在整个生命周期内的发展具有很大的随机性。本章中,在点蚀机理的研究基础上,建立点蚀萌生判据,并把点蚀分为两个不同的阶段,即点蚀的萌生和生长,分别研究这两个阶段的随机性。
一、点蚀的产生
奥氏体不锈钢表面点蚀的产生是由于钝化膜受到局部破坏,使其下的基体不断溶解造成的。在相同外部条件下,钢表面存在缺陷的钝化膜会优先破坏,钝化膜的划伤或应力集中、晶格缺陷、表面夹杂都可能是产生点蚀的起因。对于不锈钢,点蚀几乎无一例外地从硫化物夹杂部位萌生。在外加拉应力的作用下,由于夹杂物与基体材料边界处存在一定的应力集中,钝化膜会优先在应力集中程度大的地方破裂,使得硫化物与周围的基体材料之间形成缝隙,造成硫化物周围环境的改变。在局部环境的影响下,硫化物容易溶解,溶解的硫化物再附着在该位置,形成封闭的区间,封闭区内溶液成分发生变化,易于溶解基体材料,最终使点蚀形核。
在拉应力的作用下,钝化膜易修复,产生点蚀所需时间缩短,产生点蚀的概率也会增大。但是,点蚀的产生主要还是受电化学过程控制。因此,从电化学角度建立点蚀的萌生判据更加合理。
1. 点蚀产生的电化学判据
点蚀的产生与点蚀电位φp有密切关系。在实际情况中,点蚀电位是用来确定钝态金属耐点蚀能力的重要参数。由于不锈钢的点蚀优先在一些夹杂物部位形核,因此对于每个钝态金属腐蚀体系,总会存在一个临界点蚀电位φcp,即钝态金属表面上具有临界尺寸和最大活性点的平衡电位。在自腐蚀状态下,如果把临界点蚀电位作为点蚀发生的阻力,那么钝态体系的腐蚀电位φcorr则成为推动点蚀萌生的动力。当体系的腐蚀电位超过临界点蚀电位时,点蚀就可能萌生。
a. 动力
在中性、碱性及弱酸性介质中,奥氏体不锈钢点蚀与其他大多数金属的腐备一样,都属于氧去极化腐蚀。假设不锈钢在弱酸性NaCl溶液中阴极反应仅为氧的还原反应:

根据混合电位理论,在自腐蚀状态下,金属的阳极溶解电流密度ia与去极化剂阴极反应电流密度的绝对值ic相等,电化学反应步骤控制时,氧还原反应的超电位ηo可由以下公式计算:

在酸性环境中,氧还原反应的基本步骤可分为:

b. 阻力
不锈钢表面的钝化膜对基体的保护程度与钝化膜的稳定性、致密性等有关。夹杂物的存在使钝化膜产生缺陷,Cl-等侵蚀性离子很容易沉积在钝化膜缺陷处,使钝态体系的临界点蚀电位φcp降低。
目前,没有通用的理论公式来计算临界点蚀电位φcp和点蚀电位φp数值。
点蚀电位可以通过测极化曲线得到,一般把扫描速度接近于0时的测量值作为真正的点蚀电位,此时,临界点蚀电位和测量点蚀电位相差很小。因此,扫描速度为0时的点蚀电位可作为临界点蚀电位的近似值。但在实际情况中,把扫描速度设为0是不现实的。为求得真实的点蚀电位,可以对不同扫描速度下测得的φp进行线性拟合,并采用外推法,外推至扫描速度为0时的数值即为真实的点蚀电位。通过试验发现,Cl-浓度越低,扫描速度对点蚀电位的影响越小。当Cl-浓度较小时,扫描速度为10mV/min时测得的点蚀电位与扫描速度为0时的点蚀电位相近。为了减少试验数量,可以把扫描速度为10mV/min时测得的点蚀电位近似作为临界点蚀电位。
受试验条件的限制,一般测得的临界点蚀电位没考虑应力的影响,但是应力可以提高金属基体和表面氧化膜层的化学位,还会使金属表面的缺陷位置发生应力集中,从而使临界点蚀电位降低。在弹性变形范围内,因应力而引起的临界直蚀电位变化可以用下式计算:

不考虑应力集中时,由式(4-8)计算出的电位降与文献的实测值处于同一数量级。然而,MnS夹杂与基体材料相交部位会存在一定的应力集中。根据文献取应力集中系数为2,当施加240MPa(小于屈服强度)的应力时,由式(4-8)计算得到临界点蚀电位变化量ΔΦcp=-18mV.受MnS形状的影响,有些部位的应力集中系数可能远大于2,临界点蚀电位的降低量会更大。
基于以上分析,点蚀产生的准则为: φcorr > Ψcp (4-9)
2. 点蚀产生的概率分析
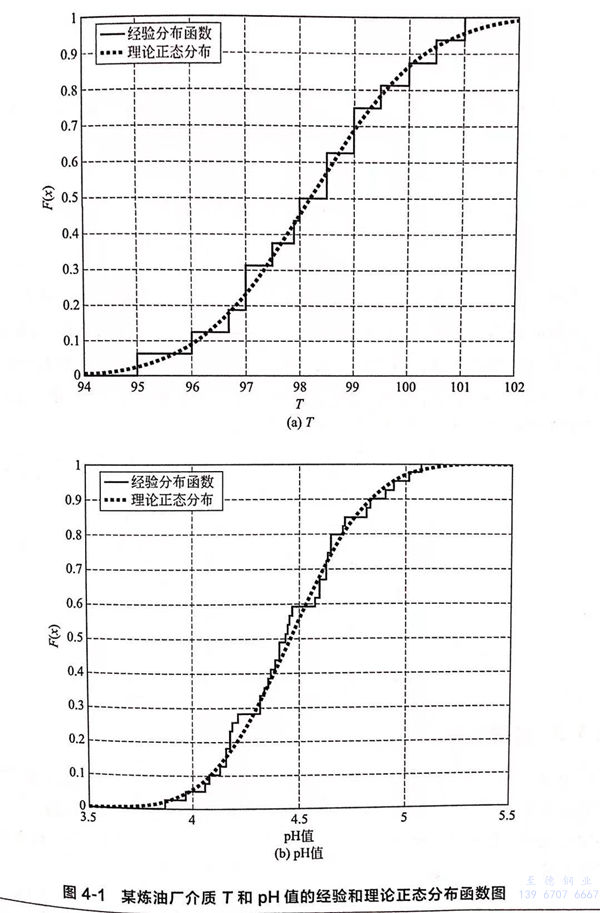
从以上分析可以看出,点蚀的产生受很多变量的影响,变量的不确定性给点蚀产生带来很大的随机性,主要的随机变量为T、pH、ib、i0以及φcp。对某炼油厂提供的监测数据进行统计分析,经过x2检验发现,在显著性水平0.05下,温度T和溶液的pH值都满足正态分布,如图4-1所示。变量φcp、ip、io的随机性需要通过试验数据统计获得。根据文献的试验结果,当Cl-浓度较小(约60mg/kg以下)时,维钝电流密度和交换电流密度变化很小,可作为确定性变量;当Cl-浓度大于60mg/kg时,分析发现,维钝电流密度和交换电流密度满足正态分布。
当考虑以上变量的随机性时,点蚀萌生概率可表示为:
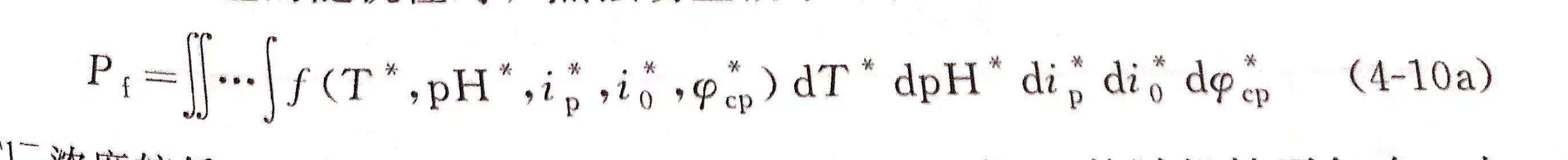
Cl-浓度较低的情况下(小于60mg/L),变量i0和ip的随机性可忽略,点蚀萌生的概率表达式为:

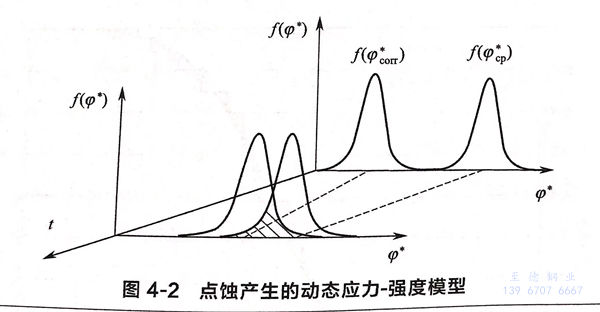
随着时间的增加,Cl-在活性点的吸附量增多,加速了钝化膜的溶解,从而使临界点蚀电位向负方向偏移。因此,临界点蚀电位随时间在数值上是减小的,即t↑→φcb(t)↓.因此,采用强度退化的动态应力-强度模型可以很好地描述点蚀产生随时间的变化关系,模型如图4-2所示。
3. 计算实例
为分析点蚀萌生概率,以304L不锈钢为试样,进行动电位极化曲线测试,材料化学成分如表4-1所示。把圆柱形试样用环氧树脂密封,只保留直径为1cm的圆形表面,经打磨、抛光、清洗、吹干后备用。电化学实验采用三电极体系,工作电极的封装过程如下:

①. 准备环氧树脂。通常是按照特定比例,混合A、B两胶。混合后的环氧树脂很黏稠。
②. 抽滤环氧树脂。用真空泵将环氧树脂中的气泡抽出。
③. 准备模具和样品。将一个PVC环平放在桌面/垫布上,将和铜导柱焊接在一起的样品倒立放置在PVC环的中央。
④. 往圆环中倒入环氧树脂,在室温下风干至少24h。
⑤. 在打磨机上对电极进行打磨抛光直至形成镜面。如样品和铜导柱之间焊接的不好,打磨的外力可能会导致接触不良,以致测试时导通不良好。
试验溶液为0.1%NaCl+CH3COOH,溶液的pH值为5左右。把试样分批次浸泡在试验溶液中,浸泡时间分别为0d、5d、25d、45d、60d、65d.把浸泡后的试样作为工作电极进行极化曲线测试,试验后部分试样表面点蚀情况如图4-3所示。室温下,由于温度波动很小,把温度作为确定性变量;介质为空气所饱和,氧分压比取0.21;对实验数据进行统计处理后,采用蒙特卡罗数值模拟法计算不同时间的点蚀萌生概率。当模拟次数大于105时,计算结果基本不随模拟次数的增加而变化。因此,把模拟次数为105时的计算结果作为最终值,结果如图4-4所示。


二、点蚀产生率分析
为了解不同时间点蚀萌生数量,采用浸泡法研究点蚀的萌生率,为缩短试验周期,使用FeCl。溶液作为腐蚀液。试验用材、试样尺寸、封装方式同4.1.3节,试样打磨后放入6%FeCl3溶液中浸泡。经过一定时间的腐蚀后,把试样取出,经清洗和烘干,在低倍镜下测量单位面积上的点蚀坑数目。点蚀密度随浸泡时间的变化趋势如图4-5所示。从图4-5可看出,点蚀产生的初始阶段,点蚀萌生率很大,经过一段时间后逐渐减小,并趋于平稳。由于点蚀的产生与材料表面的MnS夹杂有关,MnS夹杂部位点蚀的孕育时间基本相同,点蚀萌生时间比较集中。
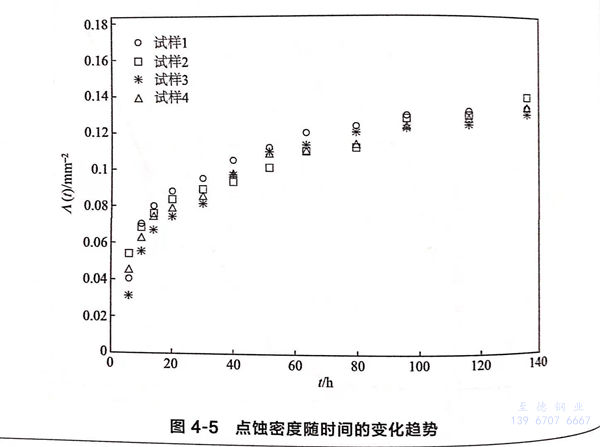
点蚀萌生率趋于平稳的原因有两方面:一方面,当材料表面绝大部分的MnS夹杂溶解并形成点蚀坑后,点蚀坑萌生速率由萌生速率平稳的光滑表面上形成的点蚀坑控制;另一方面,在已有的点蚀坑生长过程中,坑外的阴极反应抑制了点蚀坑周围钝化膜的溶解,降低了点蚀敏感性。
为了描述点蚀萌生数量与时间之间的关系,选用非齐次泊松过程来模拟点蚀的萌生过程。定义平均点蚀密度为:

根据试验数据,采用极大似然法估算γ 和 δ 值。假设第 i 个时间区间(ti-1,ti)内单位面积上萌生的点蚀数目ki,每个进行了12次观察,根据式(4-14),可得到任一试样j 上点蚀萌生数目分布的似然函数:

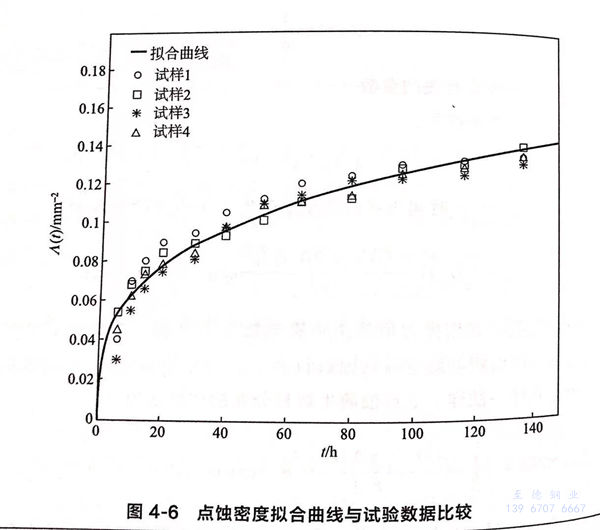
采用MATLAB软件求解,分别得到γ和8的最大似然估计值为0.0317和0.301。根据参数拟合的曲线(如图4-6所示),虽然单个试样上点蚀萌生数量与拟合结果有一定的差距,但是综合所有的试样来比较,试验值与模拟值是很接近的。因此,采用非齐次泊松过程可以很好地描述奥氏体不锈钢点蚀产生过程的随机性。
三、点蚀生长概率分析
1. 点蚀生长模型
稳态点蚀一旦形成,坑外发生阴极反应:2H2O+O2+4e- → 4OH-或H++e- → H;坑内的金属发生阳极溶解反应:M→Mn++ne-;金属离子向外扩散并会进一步发生水解反应:Mn++H2O→M(OH)(n-1)++H+。腐蚀产物和可溶性盐在坑口沉淀,使蚀坑形成闭塞电池。随着水解反应的进行,点蚀坑内溶液的酸性增强,为了保持电荷平衡,Cl-向坑内迁移,坑壁金属无法再钝化,坑内Cl-浓度逐渐升高,加速了腐蚀进程。
点蚀坑的形状有半球形、半椭球性、锥形等,其中半椭球形是奥氏体不锈钢点蚀中最常见的一种类型。假设点蚀坑的形状为半椭球形,长轴、短轴和深度分别用2b、2c、a表示,当开口平面内长、短两轴相等,即b=c时,点蚀坑的体积可写为:

点蚀坑的生长包括亚稳态和稳态两个阶段。亚稳态点蚀生长过程中,一般点蚀电流密度较大,点蚀生长较快,与整个点蚀生长过程相比较,此阶段所经历的时间很短。可以采用点蚀电流密度ip和点蚀坑深度a的乘积值来判断点蚀是否已发展到稳定状态。Pistorius等人的研究表明,当ipa值达到3×10-4A/mm时就可使点蚀坑稳定生长。根据文献的研究结果,304L不锈钢在3.5%NaCl溶液中亚稳态点蚀活性溶解阶段电流密度为3.5×10-2A/m㎡,由此可计算出稳态点蚀坑的初始深度为8.57μm。
2. 点蚀生长概率
根据式(4-22)来分析点蚀生长概率,首先需要分析表达式中的确定变量有随机变量。其中,M、z和p是确定变量,Ip、ø 和a0为随机变量。在点蚀者定生长阶段,由于不考虑形态的变化,可以只考虑Ip和a0的不确定性而忽略形状系数ø的不确定性。
a. Ip的不确定性

由于不同的环境和应力作用下Ip0无法通过计算公式得到,因此Ip的随机性只能通过对大量实测数据统计获得。
b. ao的不确定性
假设点蚀初始深度等于MnS夹杂物的横截面尺寸,那么,ao的不确定性是由夹杂物的尺寸引起的。对于奥氏体不锈钢,MnS夹杂物直径在1~5μm之间,根据文献的统计,MnS夹杂物横截面尺寸服从对数正态分布,均值和方差分别是2μm和0.1μ㎡,根据概率理论求得ao的概率密度函数为:
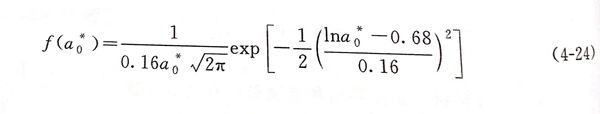
四、总结
本次主要研究了点蚀的萌生和生长,在此基础上,分析了萌生和生长的概率。
①. 分析点蚀萌生的电化学机理,建立了点蚀萌生的判据。根据试验数据;计算了点蚀萌生的概率。
②. 对304L不锈钢点蚀实验数据进行了分析,采用非齐次泊松过程描述了点蚀产生的随机过程,并对模型的参数进行了估计。
③. 对半椭球点蚀坑的生长过程进行了建模,分析了模型中变量的随机性。
结果表明,点蚀坑深度尺寸的概率主要与点蚀电流和MnS夹杂物的尺寸两个随机变量有关。



